python numpy

What is a Python NumPy?

NumPy is a Python package which stands for ‘Numerical Python’. It is the core library for scientific computing, which contains a powerful n-dimensional array object, provide tools for integrating C, C++ etc. It is also useful in linear algebra, random number capability etc. NumPy array can also be used as an efficient multi-dimensional container for generic data. Now, let me tell you what exactly is a python numpy array.

NumPy Array: Numpy array is a powerful N-dimensional array object which is in the form of rows and columns. We can initialize numpy arrays from nested Python lists and access it elements. In order to perform these numpy operations, the next question which will come in your mind is:

How do I install NumPy?

To install Python NumPy, go to your command prompt and type “pip install numpy”.

Here, I have different elements that are stored in their respective memory locations. It is said to be two dimensional because it has rows as well as columns. In the above image, we have 3 columns and 4 rows available.

Let us see how it is implemented in PyCharm:

Single-dimensional Numpy Array:

1 2 3

from numpy import * a=array([1,2,3]) print(a)

Output – [1 2 3]

Multi-dimensional Array:

1 2	a=array([(1,2,3),(4,5,6)]) print(a)

O/P – [[ 1 2 3]
[4 5 6]]

Many of you must be wondering that why do we use python numpy if we already have python list? So, let us understand with some examples in this python numpy tutorial.

Python NumPy Array v/s List

We use python numpy array instead of a list because of the below three reasons:

1. Less Memory
2. Fast
3. Convenient

The very first reason to choose python numpy array is that it occupies less memory as compared to list. Then, it is pretty fast in terms of execution and at the same time it is very convenient to work with numpy. So these are the major advantages that python numpy array has over list.

Python NumPy Operations

• ndim:
  You can find the dimension of the array, whether it is a two-dimensional array or a single dimensional array. So, let us see this practically how we can find the dimensions. In the below code, with the help of ‘ndim’ function, I can find whether the array is of single dimension or multi dimension.

1 2 3

from numpy import * a = array([(1,2,3),(4,5,6)]) print(a.ndim)

Output – 2
Since the output is 2, it is a two-dimensional array (multi dimension).

• itemsize:
  You can calculate the byte size of each element. In the below code, I have defined a single dimensional array and with the help of ‘itemsize’ function, we can find the size of each element.

  1 2 3

  from numpy import * a = array([(1,2,3)]) print(a.itemsize)

  Output – 4
  So every element occupies 4 byte in the above numpy array.
• dtype:
  You can find the data type of the elements that are stored in an array. So, if you want to know the data type of a particular element, you can use ‘dtype’ function which will print the datatype along with the size. In the below code, I have defined an array where I have used the same function.

1 2 3

from numpy import * a = array([(1,2,3)]) print(a.dtype)

Output – int32

As you can see, the data type of the array is integer 32 bits. Similarly, you can find the size and shape of the array using ‘size’ and ‘shape’ function respectively.

Output – 6 (1,6)

Next, let us move forward and see what are the other operations that you can perform with python numpy module. We can also perform reshape as well as slicing operation using python numpy operation. But, what exactly is reshape and slicing? So let me explain this one by one in this python numpy tutorial.

• reshape:
  Reshape is when you change the number of rows and columns which gives a new view to an object. Now, let us take an example to reshape the below array:
   
  As you can see in the above image, we have 3 columns and 2 rows which has converted into 2 columns and 3 rows. Let me show you practically how it’s done.

  1 2 3 4 5

  from numpy import * a = array([(8,9,10),(11,12,13)]) print(a) a=a.reshape(3,2) print(a)

  Output – [[ 8 9 10] [11 12 13]] [[ 8 9] [10 11] [12 13]]
• slicing:
  As you can see the ‘reshape’ function has showed its magic. Now, let’s take another operation i.e Slicing. Slicing is basically extracting particular set of elements from an array. This slicing operation is pretty much similar to the one which is there in the list as well. Consider the following example:
  
  Before getting into the above example, let’s see a simple one. We have an array and we need a particular element (say 3) out of a given array. Let’s consider the below example:

  1 2 3

  import numpy as np a=np.array([(1,2,3,4),(3,4,5,6)]) print(a[0,2])

  Output – 3
  
  Here, the array(1,2,3,4) is your index 0 and (3,4,5,6) is index 1 of the python numpy array. Therefore, we have printed the second element from the zeroth index.
  Taking one step forward, let’s say we need the 2nd element from the zeroth and first index of the array. Let’s see how you can perform this operation:

  1 2 3

  import numpy as np a=np.array([(1,2,3,4),(3,4,5,6)]) print(a[0:,2])

  Output – [3 5]
  
  Here colon represents all the rows, including zero. Now to get the 2nd element, we’ll call index 2 from both of the rows which gives us the value 3 and 5 respectively.
  Next, just to remove the confusion, let’s say we have one more row and we don’t want to get its 2nd element printed just as the image above. What we can do in such case?
  Consider the below code:

  1 2 3

  import numpy as np a=np.array([(8,9),(10,11),(12,13)]) print(a[0:2,1])

  Output – [9 11]
  
  As you can see in the above code, only 9 and 11 gets printed. Now when I have written 0:2, this does not include the second index of the third row of an array. Therefore, only 9 and 11 gets printed else you will get all the elements i.e [9 11 13].
• linspace
  This is another operation in python numpy which returns evenly spaced numbers over a specified interval. Consider the below example:

  1 2 3

  import numpy as np a=np.linspace(1,3,10) print(a)

  Output – [ 1. 1.22222222 1.44444444 1.66666667 1.88888889 2.11111111 2.33333333 2.55555556 2.77777778 3. ]
  
  As you can see in the result, it has printed 10 values between 1 to 3.
• max/ min
  Next, we have some more operations in numpy such as to find the minimum, maximum as well the sum of the numpy array. Let’s go ahead in python numpy tutorial and execute it practically.

  1 2 3 4 5 6

  import numpy as np a= np.array([1,2,3]) print(a.min()) print(a.max()) print(a.sum())

  Output – 1 3 6
  
  You must be finding these pretty basic, but with the help of this knowledge you can perform a lot bigger tasks as well. Now, lets understand the concept of axis in python numpy.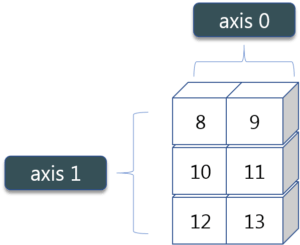
  
  
  
  
  As you can see in the figure, we have a numpy array 2*3. Here the rows are called as axis 1 and the columns are called as axis 0. Now you must be wondering what is the use of these axis?
  Suppose you want to calculate the sum of all the columns, then you can make use of axis. Let me show you practically, how you can implement axis in your PyCharm:

  1 2	a= np.array([(1,2,3),(3,4,5)]) print(a.sum(axis=0))

  Output – [4 6 8]
  
  Therefore, the sum of all the columns are added where 1+3=4, 2+4=6 and 3+5=8. Similarly, if you replace the axis by 1, then it will print [6 12] where all the rows get added.
• Square Root & Standard Deviation
  There are various mathematical functions that can be performed using python numpy. You can find the square root, standard deviation of the array. So, let’s implement these operations:
  

  1 2 3 4

  import numpy as np a=np.array([(1,2,3),(3,4,5,)]) print(np.sqrt(a)) print(np.std(a))

  Output – [[ 1. 1.41421356 1.73205081]
  [ 1.73205081 2. 2.23606798]]
  1.29099444874
  
  
  As you can see the output above, the square root of all the elements are printed. Also, the standard deviation is printed for the above array i.e how much each element varies from the mean value of the python numpy array.
• Addition Operation
  
  You can perform more operations on numpy array i.e addition, subtraction,multiplication and division of the two matrices. Let me go ahead in python numpy tutorial, and show it to you practically: 

  1 2 3 4

  import numpy as np x= np.array([(1,2,3),(3,4,5)]) y= np.array([(1,2,3),(3,4,5)]) print(x+y)

  Output – [[ 2 4 6] [ 6 8 10]]
  
  This is extremely simple! Right? Similarly, we can perform other operations such as subtraction, multiplication and division. Consider the below example:

  1 2 3 4 5 6

  import numpy as np x= np.array([(1,2,3),(3,4,5)]) y= np.array([(1,2,3),(3,4,5)]) print(x-y) print(x*y) print(x/y)

  Output – [[0 0 0] [0 0 0]]
  [[ 1 4 9] [ 9 16 25]]
  [[ 1. 1. 1.] [ 1. 1. 1.]]
• Vertical & Horizontal Stacking
  Next, if you want to concatenate two arrays and not just add them, you can perform it using two ways – vertical stacking and horizontal stacking. Let me show it one by one in this python numpy tutorial.

  1 2 3 4 5

  import numpy as np x= np.array([(1,2,3),(3,4,5)]) y= np.array([(1,2,3),(3,4,5)]) print(np.vstack((x,y))) print(np.hstack((x,y)))

  Output – [[1 2 3] [3 4 5] [1 2 3] [3 4 5]]
  [[1 2 3 1 2 3] [3 4 5 3 4 5]]